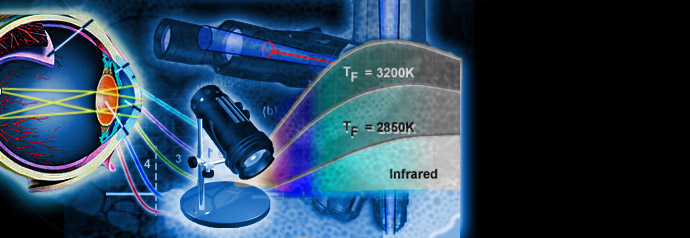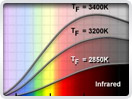
Physics of Light and Color
Light is a complex phenomenon that is classically explained with a simple model based on rays and wavefronts. The Olympus Microscopy Resource Center Microscopy Primer explores many of the aspects of visible light starting with an introduction to electromagnetic radiation and continuing through to human vision and the perception of color.
Basic Concepts in Optical Microscopy
Microscopes are instruments designed to produce magnified visual or photographic images of small objects. The microscope must accomplish three tasks: produce a magnified image of the specimen, separate the details in the image, and render the details visible to the human eye or camera.

Specialized Microscopy Techniques
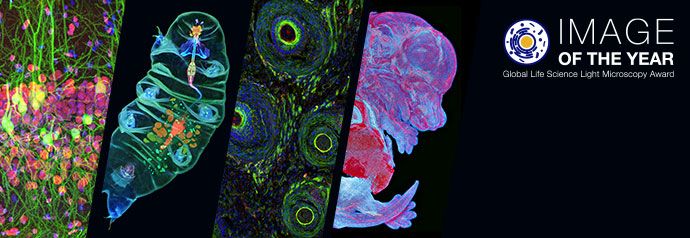
Fluorescence illumination and observation is the most rapidly expanding microscopy technique employed today, both in the medical and biological sciences, a fact which has spurred the development of more sophisticated microscopes and numerous fluorescence accessories.
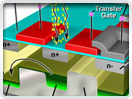
Digital Imaging in Optical Microscopy
Digitization of a video or electronic image captured through an optical microscope results in a dramatic increase in the ability to enhance features, extract information, or modify the image. When compared to the traditional mechanism of image capture, photomicrography on film, digital imaging and post-acquisition processing enables a reversible, essentially noise-free modification of the image as an ordered matrix of integers rather than a series of analog variations in color and intensity.

Photomicrography
The use of photography to capture images in a microscope dates back to the invention of the photographic process. Early photomicrographs were remarkable for their quality, but the techniques were laborious and burdened with long exposures and a difficult process for developing emulsion plates.